Poids de Hamming

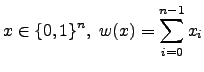
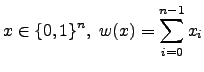
Le full adder (FA) est l'élément essentiel du circuit proposé par Muller et Preparata dans [#!muller:1975!#]. Un (FA) est un additionneur 2-bit avec une retenue entrante, il est composé essentiellement de deux half adder (HA), additionneur 2-bit sans retenue entrante, ce dernier prend en entrée deux bits et il sort leur somme et leur retenue. Les deux figures qui suivent représentent respectivement un (HA) et un (FA).

Figure: Half Adder.

= =

Figure: Full adder.

= = ( ) ( ) ( )

• Présentation du circuit:
  Il est très facile de construire, à partir de full adder, un circuit qui permet de calculer le poids de Hamming de bits en entrée. Un full adder prend en entrée trois bits or, pour la construction de notre fonction de filtrage, nous avons besoin de sept entrées correspondant aux sept bits filtrés par la fonction .
  

  Un tel circuit se comporte suivant la formule suivante:
  

  Exemple pour =7
  

  			(1)

  
  

  avec = , = , = , : la sortie et : la retenue.
  

  On obtient donc le circuit suivant:
  

  Figure: Le poids de Hamming avec un circuit.

  Certaines machines disposent d'instructions permettant de calculer directement le poids de Hamming d'un mot machine (comme les alpha evo67, les itanium...). Pour les machines qui ne disposent pas de telles instructions, le programmeur doit les émuler. Il existe plusieurs méthodes pour calculer le poids de Hamming.
  Pour notre programme, nous avons implémenté cinq méthodes différentes.
  

• La méthode naive :
  Elle est assez simple elle consiste à regarder chaque bit de la séquence et à incrémenter le poids de Hamming si le bit est à 1. Le point faible de cette méthode réside dans le fait que l'on doit parcourir tout le mot.

  Figure: La méthode naive.

• La méthode arithmétique :
  Elle consiste à éliminer successivement le dernier 1 de la séquence.
  Exemple
  
  

  La complexité de l'algorithme dépend du nombre de 1 dans la séquence. Cette méthode est nettement plus efficace vu que le nombre de boucles à effectuer est égale au nombre de 1. Bien évidemment s'il n'y a que des 1 dans un mot de taille , on effectuera boucles.
  

  Figure: La méthode arithmétique.

• La mise en table :
  L'idée est assez simple, on utilise l'un des deux algorithmes expliqués précédemment pour créer des tables qui contiennent le poids de Hamming de tous les mots sur 4, 8 ou 16 bits. On effectue par la suite des accès en table. L'avantage est que le calcul effectif sur le processeur est quasi absent, mais on doit faire des accès mémoires. Il n'est pas envisageable de faire des mises en table pour des séquences de 32 bits (ce qui correspond à une table de 4Go). Comme dans la pratique on travaille sur la taille des mots machines, on peut faire des mises en table pour 8 et 16 bits. Au sens algorithmique, cette méthode ne coûte que ou additions. On va voir par la suite au moment des tests que le coût des accès mémoire n'est pas null. Les performances de cette méthode peuvent être catastrophiques suivant les caractéristiques de la mémoire cache de la machine.
  
• Diviser pour règner :
  Cette méthode consiste à subdiviser la séquence puis à regrouper successivement les données. On calcule d'abord tous le poids de tous les sous mots de taille 2 bits. On isole un bit sur deux de la séquence puis on isole indépendemment les bits restants. On les additionne et on obtient ainsi leur poids sur 2 bits. On recommence ainsi de suite avec des paquets de bits toujours plus grands (x2).
  

  Figure: Diviser pour règner sur un mot de 8 bits.

Emulation du circuit
Le circuit présenté à la figure permet de faire un calcul parallèle en faisant correspondre chaque fil d'entrée du circuit à un bit. L'avantage est de calculer en parallèle le poids de Hamming de 7 mots de 32 bits, l'idée est de faire tourner le circuit seulement 32 fois pour tous les mots.